재귀 함수

탐색

많은 데이터 중에서 원하는 데이터를 찾는 과정

특정 조건에 맞는 데이터 존재하는지 만약 존재한다면 어떤 위치에 존재하는지 찾는다.

 

 

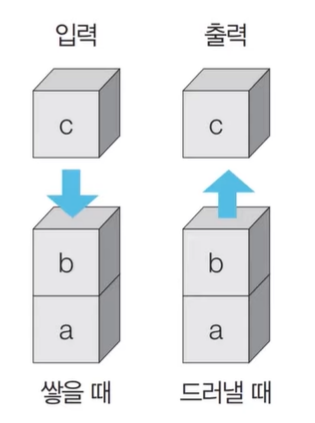
스택

먼저 들어온 데이터가 나중에 나가는 선입후출

박스 느낌

 

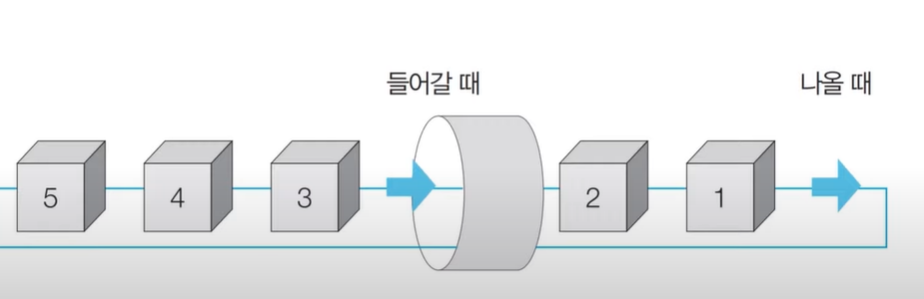
큐

먼저 들어온 데이터가 먼저 나가는 선입선출

터널 느낌

 

재귀 함수(Recursive)

- 자기 자신을 다시 호출 

- 잘 활용하면 복잡한 알고리즘을 간결하게 작성할 수 있다.

- 함수가 실행시 함수들의 정보가 스택프레임에 쌓여서 메모리에 올라감.

    ->컴퓨터 구조 측면에서 보았을 때, 스택 자료구조와 동일 그래서 스택 라이브러리 대신 재귀함수 이용하는 경우 많다.

 

- 문제 풀이에서 사용할 때는 재귀 함수의 종료 조건을 반드시 명시

    -> 명시하지 않으면 함수 무한 호출

- 모든 재귀 함수는 반복문을 이용하여 동일한 기능을 구현할 수 있다.

 

def recursive_function(i):
    # 10번째 호출을 했을 때 종료되도록 종료 조건 명시
    # i가 10이면 함수 호출하지 않고 종료
    if i == 10:
        return

    print(i, '번째 재귀함수에서', i + 1, '번째 재귀함수를 호출합니다.')
    recursive_function(i + 1) #다시 호출

    print(i, '번째 재귀함수를 종료합니다.')


recursive_function(2) #함수호출

출력

 

 

팩토리얼

0!, 1! = 1

# 반복적으로 구현한 n!
def factorial_iterative(n):        
    result = 1
    # 1부터 n까지의 수를 차례대로 곱하기
    for i in range(1, n + 1):
       result *= i
    return result

# 재귀적으로 구현한 n!
def factorial_recursive(n):        
    if n <= 1: # n이 1 이하인 경우 1을 반환
        return 1
    # n! = n * (n - 1)!를 그대로 코드로 작성하기
    return n * factorial_recursive(n - 1)

# 각각의 방식으로 구현한 n! 출력(n = 5)
print('반복적으로 구현:', factorial_iterative(5))
print('재귀적으로 구현:', factorial_recursive(5))


"""
반복적으로 구현: 120
재귀적으로 구현: 120
"""

 

 

유클리드 호제법

- 재귀함수를 효과적으로 사용

- 두 개의 자연수에 대한 최대공약수 구하는 알고리즘

- 두 자연수 A,B에 대하여 (A>B) A를 B로 나눈 나머지를 R이라고 할 때,

   A,B의 최대공약수는 B, R의 최대공약수와 같다.

 

GCD = 최대공약수

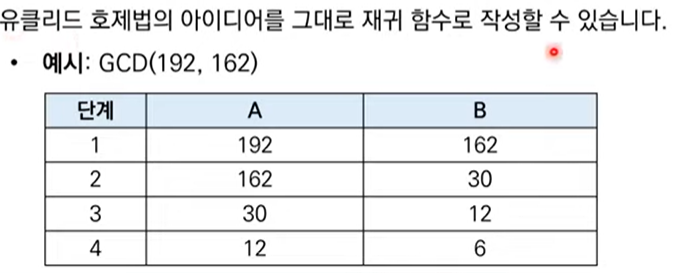
192와 162의 최대공약수를 구하는 법

192%162=30(나머지) 을 구한뒤  162와 30의 최대 공약수와 같은 값을 가진다.

결과적으로 12, 6의 최대공약수와 같다

 

def gcd(a,b):
  if a % b ==0:
    return b
  else:
    return gcd(b, a%b)

print(gcd(192,162)) #6

 

 

 

 

 

https://www.youtube.com/watch?v=7C9RgOcvkvo&list=PLRx0vPvlEmdAghTr5mXQxGpHjWqSz0dgC&index=3