PYTHON/데이터분석
통계 데이터 분석 -선형회귀
sshhhh
2023. 9. 15. 17:15
#참고자료
https://hleecaster.com/ml-linear-regression-concept/
선형회귀(Linear Regression) 쉽게 이해하기 - 아무튼 워라밸
본 포스팅에서는 머신러닝에서 사용할 선형 회귀 분석에 대한 개념 설명을 누구나 이해할 수 있을 정도의 수준으로 가볍게 소개한다. (머리 나쁜 나도 이해한 수준까지만 설명할 거니까 대부분
hleecaster.com
03) 선형 회귀(Linear Regression)
딥 러닝을 이해하기 위해서는 선형 회귀(Linear Regression)와 로지스틱 회귀(Logsitic Regression)를 이해할 필요가 있습니다. 이번 챕터에서는 머 ...
wikidocs.net
선형회귀
import matplotlib.pyplot as plt
ex_xs = [[2],[4],[7],[1],[9],[6]] #독립변수 6개
ex_ys = [8,11,24,5,30,20] #종속변수 6개
plt.plot(ex_xs, ex_ys, 'o', label = "example data")
plt.xlabel("x")
plt.ylabel("y")
plt.legend()
plt.show()
plt.figure(figsize=(5,5)) #표사이즈
plt.plot(ex_xs[:], ex_ys, 'o', label = "example data")
plt.plot([0,30], [0*2+2, 30*2+2], label = "y=2x+2")
plt.plot([0,30], [0*3+2, 30*3+2], label = "y=3x+2")
plt.plot([0,30], [0*4+2, 30*4+2], label = "y=4x+2")
plt.xlabel("x")
plt.ylabel("y")
plt.legend() #범례
plt.xlim(0,30)
plt.ylim(0,30)
plt.show()


import numpy as np
def mse(yp, y): #yp:예측값, y:실제값
"""
(예측값-실제값)의 제곱의 평균을 구하는 손실함수
"""
return np.mean(sum(yp-y)**2)
b=2 #편향 2
mses=[]
wpl=np.arange(-10,10,0.5) #가중치 -10~10까지 0.5씩 증가
for wp in wpl:
yp = wp*np.array(ex_xs)+b #예측값
mses.append(mse(yp,ex_ys))
mi = np.array(mses).argmin() #최솟값이 있는 인덱스
plt.plot(wpl, mses, '.')
plt.plot(wpl[mi], mses[mi], 'or') #최솟값
plt.xlabel('w')
plt.ylabel('mse')
plt.show()
print(wpl[mi])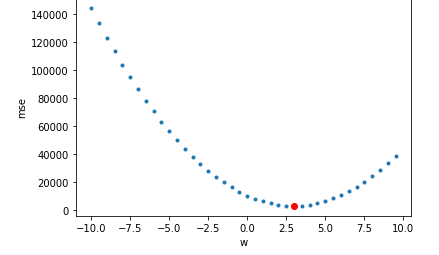
경사하강법
파라미터를 임의로 정한 다음에 조금씩 변화시켜가며 손실을 점점 줄여가는 방법으로 최적의 파라미터를 찾아간다.
def gradient(y,x,w,b):
yp = w*x+b
error = y-yp
wd = (2*sum(error*x)/len(x))
bd = (2*sum(error)/len(x))
return wd, bd
from re import A
def gradient_descent(x,y,lr=0.001, epochs=100):
"""
경사하강법 함수
입력 매개변수 : x,y,lr,epochs
x:독립변수
y:종속변수
lr:경사를 이동시킬 때 사용할 비율(lr*경사만큼 이동)
epochs:학습횟수
"""
if isinstance(x,list): #x가 list일 때
x=np.array(x).reshape(-1) #1차원 numpy 배열로 변화
wbhl = [] #학습과정을 기록할 컬렉션
wp = np.random.uniform(-1, 1) #가중치 초기값을 -1~1 사이의 랜덤 값으로 지정
bp = np.random.uniform(-1, 1) #편향 초기값을 -1~1 사이의 랜덤 값으로 지정
amse = 0 #경사를 조절한 후에 mse를 기억할 변수를 0으로 초기화
for epoch in range(epochs): #epochs 횟수만큼 학습시킨다.
bmse = amse #이전 mse로 설정
wd, bd = gradient(y, x, wp, bp) #경사를 구함(여기에서는 경사에 -부호를 취한 값)
yp = wp*x + bp #예측
amse = mse(yp, y) #새로 계산한 mse값
wp = wp-(wd*lr) #가중치를 조절
bp = bp-(bd*lr) #편향을 조절
wbhl.append([wp, bp]) #히스토리에 가중치와 편향을 보관
if np.abs(bmse-amse)<0.001: #이전 mse와 이후 mse의 차이가 정해준 값보다 작다면
break #더 이상 학습하지 말고 반복문 탈출
return wp,bp,wbhl #가중치, 편향, 히스토리 반환wp,bp,wbhl = gradient_descent(ex_xs,ex_ys)
for epoch, (ewp,ebp) in enumerate(wbhl):
print(f'epoch:{epoch} w:{ewp} b:{ebp}')
"""
epoch:0 w:0.4930876976778227 b:-0.14754404334826426
epoch:1 w:0.31473057174737373 b:-0.17573928369074185
epoch:2 w:0.12498329764394955 b:-0.20571503339789873
epoch:3 w:-0.07688132212575727 b:-0.23758495825413636
.
.
.
epoch:98 w:-1199.9050577891892 b:-187.80939961493792
epoch:99 w:-1276.7222972543263 b:-199.81676730612995
"""
xs = np.array(ex_xs)
xs = xs[: ,0] #1차원배열
ys = np.array(ex_ys)
min_val = min(min(xs), min(ys))
max_val = max(max(xs), max(ys))
for epoch, wb in enumerate(wbhl):
plt.figure(figsize=(6,6))
sx = min_val
sy = sx*wb[0] + wb[1]
ex = max_val
ey = ex*wb[0] + wb[1]
plt.plot(xs,ys,'.',label='actural')
plt.plot([sx,ex],[sy,ey],'r-',label=f'epoch:{epoch} y={wb[0]}*x+{wb[1]}')
plt.axvline(x=0, color='black')
plt.axhline(y=0, color='black')
plt.xlim(min_val, max_val)
plt.ylim(min_val, max_val)
plt.legend()
plt.show()

